初めて異常干支という言葉を聞いた時・・・何か少し不安を感じました。ちょっと言葉が怖かったのです。
異常って・・・異常干支はいきづらいのか・・・。
普通ではないということは、
どういうこと?
どういう人のことを言うのだろうと、頭の中はぐるぐると妄想状態・・・
10年以上算命学を研究し、たくさんの生徒さんに算命学を伝えている先生も、初めは言葉がきついと思われていたそうです。
皆、同じですよね!
けれど、この異常干支は立派な個性であるということをしっかりと教えていただきましたので、今日はこの異常干支の種類や特徴についてお伝えしようと思います。
干支を活用されている方は、たくさんおられます。
SBIホールディングス社長北尾吉孝氏は
毎年、最初の出社日に干支学を元に30分程度話をされるそうです。
下記の干支を中心とした本も書かれています。
異常干支が回る年は、世の中に変動が多くなります。
直近では、2018年戊戌、2019年己亥、2020年庚子という異常干支が回りました。
異常干支は生きづらい?種類は?
全部で13種類です。
甲戌・乙戌・丙戌・丁巳・丁亥・戊子・戊戌
己亥・庚子・辛巳・辛亥・壬子・癸巳
ご自身の命式に異常干支があるかどうか、気になるかと思います。
下記のサイトで検索できます。
上記の13種類の干支は、どの場所にでてきても異常干支となります。(年干支、月干支、日干支度の場所でも)
日干支の場所に異常干支が出る場合が、一番強く現象が現れます。
異常干支は生きづらい?意味は?
この異常干支があるからといって、いい現象がでるとか、悪い現象がでるというものではないです。
個性として捉えていただければいいと思います。
例えば、特別に絵を描くのが上手な子供さんの場合、算命学では、絵の才能が「異常」ということになります。
普通の才能ではないということです。
特別に絵が上手だから絵の才能が異常なのですね。

ピアノが上手な方も「異常」ということになります。
つまり、普通ではない状態のことを「異常」と表現しているのです。
決して、異常だから大変なんだ~と、解釈しないでくださいね。

よく学校の先生が「今年の2年生の学年は大人しい。」とか、「今年の3年生は本当に荒れている・・。」など表現することがあると思います。
同級生は、ほとんど同じ年干支!!になるので、命式の一部が同じということ。
その学年の生徒は、似通った一面を持ち合わせることになります。
異常干支の特徴は?
ひと口に異常干支と言いましても、それぞれに性質があります。
例えば、戊戌や丙戌の異常干支をもつ方。
戊戌、丙戌の方は、高い教養を身に付けると、ものの考え方が一般的な常識からはなれた考え方をするようになる一面があります。
世間では、「教養がある」とか、「学問の知識がある」と聞くと、うらやましいな、頭のいい人なんだろうなと勝手に想像しがち。
そして「勉強がよくできる」場合、学歴をつけてハイレベルな学校へ進学を考えます。
けれど、この戊戌や丙戌を日干支に持つ人は、特に教養をつけたりせず、普通のざっくばらんな生活を送るほうが真面目な普通の人になるとされています。
異常干支の一部を紹介しました。
異常干支・十二支別に考える
異常干支を十二支別に並び変えてみます。
どの十二支に
異常干支が多いかな~?
亥の異常干支が4個あり、一番多いです。
乙亥 丁亥 己亥 辛亥
その次に多いのは、戌です。
甲戌 丙戌 戊戌
そして巳も3個あります。
丁巳 辛巳 癸巳
続いて子。
戊子 庚子
ひとつだけあるのが午。
壬午
これで13個!!
「法則性あるのかな~」とか、「なんで、これが異常干支になるのかな~」など、 最初はわかりにくいと思います。
けれども十干別、干支番号順、十二支別、天中殺別など、並び替えたり眺めたりしているうちに、少しずつ理解が深まると思います。
暗号異常干支とは?
種類
7種類あります。
丙戌・丁亥・戊子・己亥・辛巳・壬午・癸巳
暗号異常干支の定義
干支の蔵干に注目します。
十干と十二支の蔵干が干合するものが、暗号異常干支となります。
例えば、丙戌の場合。戌の蔵干は、辛、丁、戊です。
丙と干合するものは、辛です。
(下記の赤丸です)
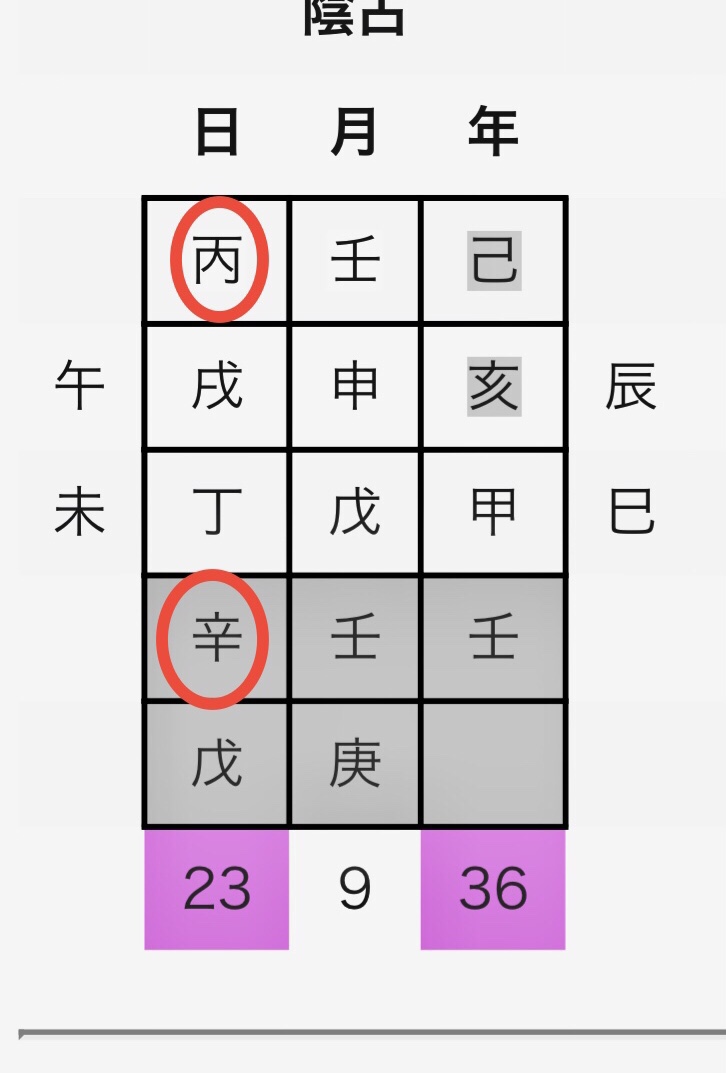
戌の中に丙の干合する辛があるから暗号異常干支になるということです。
特徴
ほかの異常干支よりも特徴がより強く出ます。
大運で異常干支が回ってくると、もともと命式に異常干支を持っている人は異常性が出にくくなるといわれています。

まとめ
「異常干支は生きづらい?種類や特徴についても!」についてお伝えしました。
異常干支のことを簡単にまとめます。
- 異常干支は個性的
- 異常干支は13種類
- 13種類それぞれに特徴あり
- 暗合異常干支は特徴が強く出る
異常干支は何か悪いもののようだというイメージを持たれるかたも多いですが、個性として捉えていただければいいかと思います。
では(^^♪
\基礎からわかる算命学/








